LearningBox
Diagram Kendali
Compiled by: Suprapto van Plaosan
Run in Google Colab

Control Chart disebut juga sebagai diagram Shewhart, diagram kontrol proses statistik (Statistical Process Control/SPC).

Diagram kontrol adalah diagram yang memeriksa bagaimana suatu proses berubah seiring waktu. Data dicatat dalam urutan kronologis. Diagram kontrol selalu memiliki garis tengah untuk rata-rata, garis atas untuk batas kontrol atas dan garis bawah untuk batas kontrol bawah. Garis-garis ini ditentukan dari data historis. Dengan membandingkan data saat ini dengan garis-garis ini, kita dapat menarik kesimpulan, apakah variasi proses konsisten (terkendali) atau tidak. Apakah hasil proses dapat diprediksi (dapat dikendalikan atau tidak (di luar kendali, dipengaruhi oleh suatu variasi). Alat pengumpulan dan analisis data serbaguna ini dapat digunakan di berbagai bidang dan dianggap sebagai salah satu dari tujuh piranti dasar pengendalian kualitas.

  • Cause-and-effect diagram (also called Ishikawa or fishbone diagrams): Mengindentifikasi kemungkinan-kemungkinan penyebab dari suatu kejadian atau masalahdan mengurutkan kemungkinan-kemungkinan tersebut menurut kategori tertentu.

  • Check sheet: Form yang terstruktur untuk mengumpulkan dan menganalisis data.

  • Control chart: Grafik yang digunakan untuk memonitor proses sebagai fungsi waktu. Perbandingan data saat ini dengan data-data sebelumnya untuk mendapatkan kesimpulan apakah data yang idapat konsisten dengan acuan yang dipakai atau bersifat tidak dapat diprediksi.

  • Histogram: Grafik untuk menunjukan distribusi frekuensi.

  • Pareto chart: Bar chart untuk melihat faktor mana yang lebih signifikan.

  • Scatter diagram: Grafik pasangan data untuk melihat hubungan antara sumbu x dan sumbu y.

  • Stratifikasi: Teknik untuk memisahlkan data dari berbagai sumber agar sehingga pola dari data dapat diamati.

Diagram kontrol variabel data terdiri dari nilai rata-rata data, nilai rata ditambah atau dikurangi beberapa kali nilai simpangan baku dari proses yang disebut sebagai UCL (upper control level) dan LCL (lower control level).

Dr. Walter A. Shewhart pada Tahun 1920 mengembangkan diagram kontrol dengan rumus umum sebagai berikut:

$$UCL = \mu_w + k \sigma_w$$$$Center Line = \mu_w$$$$LCL = \mu_w - k \sigma_w$$

Shewhart Control Charts untuk variabel w mempunyai rata-rata nilai hasil pengukuran $\mu_w$ dan simpangan baku $\sigma_w$.

umumnya metode 3 sigma digunakan sebagai nilai k (k = 3).

$\sigma_w$ adalah simpangan baku rata-rata yang diperoleh dari simpangan baku data m sebanyak n dirata-rata.

Bila $\sigma^2$ adalah variansi dari probabilitas distribusi data, maka unbiased estimator untuk $\sigma^2$ adalah sampel variansi yang diperoleh menggunakan persamaan berikut:

$$s^2 = {\frac{1}{{N - 1}}\sum\limits_{i = 1}^N {\left( {x_i - \bar x} \right)^2}}$$

Namun s adalah simpangan baku sampel dan bukan unbiased estimator dari $\sigma$. Bila diasumsikan distribusi data adalah normal, maka estimator aktual $c_4$ . $\sigma$ digunakan. Dimana $c_4$ adalah konstanta yang nilainya tergantung pada ukuran sampel n. Tabel c4 tersedia di buku statistik dan dapat dihitung menggunakan persamaan berikut:

$$c_4 = \sqrt{\frac{2}{n-1}} \frac{ \left( \frac{n}{2}-1 \right)!} {\left( \frac{n-1}{2}-1 \right)!} \, .$$

Nilai $c-4$ faktor untuk n = 10 adalah 0.9727.

Rata-rata atau nilai deviasi standar adalah $c-4 . \sigma$

Simpangan baku dari simpangan baku sampel adalah

$$\sigma_s = \sigma $$

UCL bisa juga dihitung dari

$$ \pm 3s/c_4$$

Control Charts Individual

Diagram kendali untuk pengukuran tunggal, ukuran sampel = 1, variabilitasnya dihitung dari selisih dari dua pengukuran yang berurutan.

$$\begin{eqnarray} UCL & = & \bar{x} + 3\frac{\overline{MR}}{1.128} \\ \mbox{Center Line} & = & \bar{x} \\ LCL & = & \bar{x} - 3\frac{\overline{MR}}{1.128} \, , \end{eqnarray}$$

di mana ${\bar{x}}$ adalah rata-rata dari data, $MR$ adalah rata-rata selisih antara dua pengamatan berurutan. Nilai $d_2$ untuk $n$ = 2 adalah 1,128.

Beikut adalah contoh pengukuran 10 data flowrate
0 49.6
1 47.6
2 49.9
3 51.3
4 47.8
5 51.2
6 52.6
7 52.4
8 53.6
9 52.1

Perbedaan antar data flowrate adalah

array([[2. , 2.3, 1.4, 3.5, 3.4, 1.4, 0.2, 1.2, 1.5]])

Nilai rata-rata flowrate adalah

Flowrate    50.81
dtype: float64

Nilai rata-rata selisihnya adalah sebesar

1.8777777777777784

Sehingga nilai UCL-nya adalah

Flowrate    55.80409
dtype: float64

UWL

Flowrate    54.139393
dtype: float64

LCL

Flowrate    45.81591
dtype: float64

LWL

Flowrate    47.480607
dtype: float64

Diagram kendali yang didapat adalah sebagai berikut

<matplotlib.legend.Legend at 0x7fedb9cf7490>
  • Misalnya kita mempunyai 100 data pengukuran kadar air pada Biosolar yang di produksi di suatu perusahaan.
  • Sebagai informasi awal, kadar air maksimal yang diperbolehkan ada di biosolar adalah 500 mg/Kg (ASTM standard D6751).

Berikut adalah 100 data hasil pengukuran water content dalam biodisel:

array([494, 496, 489, 487, 491, 492, 496, 492, 487, 498, 499, 492, 485,
       493, 486, 486, 492, 492, 494, 497, 490, 489, 497, 489, 491, 489,
       491, 493, 492, 490, 490, 496, 491, 497, 496, 488, 488, 492, 486,
       499, 492, 496, 493, 488, 491, 485, 495, 490, 488, 488, 498, 495,
       488, 491, 491, 498, 495, 497, 498, 492, 495, 490, 496, 496, 487,
       486, 497, 493, 498, 498, 493, 489, 486, 490, 489, 497, 492, 496,
       497, 485, 490, 486, 488, 491, 488, 493, 488, 485, 491, 493, 489,
       495, 496, 490, 487, 487, 497, 495, 495, 489])

Histogram 100 data tersebut ditampilkan pada Gambar di bawah ini

<AxesSubplot:>

Data deskriptif statistik untuk 100 data tersebut dirangkum dalam tabel berikut:

0
count 100.000000
mean 491.840000
std 3.927937
min 485.000000
25% 489.000000
50% 492.000000
75% 495.250000
max 499.000000

Dari data deskriptif statistik bisa digambarkan pada Boxplot di bawah ini. Terlihat bahwa nilai min 472.234661 merupakan outlier. IQ1 (25%) = 488.750000, Median = 492.000000 dan IQ3 (75%) = 496.000000

<AxesSubplot:>

Control Chart dibuat dengan menggunakan nilai rata-rata sebagai garis horisontal di tengah,

UCL/upper control level, batas control atas : garis yang berwarna biru

$${\bar x} + {2\sigma}$$

LCL/lower control level, batas control bawah

$${\bar x} - {2\sigma}$$

.

UWL/upper warning level, batas peringatan atas :

$${\bar x} + {3\sigma}$$

dan LWL/lower warning level :

$${\bar x} - {3\sigma}$$ 
<matplotlib.legend.Legend at 0x7fedb9a37250>

Dari segi aplikasi, control chart yang sebenarnya kita butuhkan untuk kasus di atas hanyalah batas kontrol atas (UCL) dengan nilai sebesar 500,sebagaimana disyaratkan dalam ASTM. Misalnya kita tetapkan untuk memberi batas warning atas 5 point sebelum angka maksimal yang diijinkan, maka UWL yang kita pasang aadalah 495. Sehingga untuk riil kontrol chart yang berguna untuk proses kita, kita bisa mengubah kontrol chart di atas sebagai berikut:

<matplotlib.legend.Legend at 0x7fedb9a2ff10>

EWMA Control Charts

EWMA (Exponentially Weighted Moving Average) adalah metode statistik untuk memonitoring proses menggunakan FIIR (first-order infinite impulse response) filter. FIIR filter membuat pengaruh data semakin menurun secara exponensial dengan berjalannya waktu namun tidak pernah mencapai angka nol.

$$_t = \lambda Y_t + (1-\lambda) _{t-1} \,\,\, \,\,\, t = 1, \, 2, \, \ldots,\, n$$
  • $EWMA_0$ adalah rata-rata data target
  • $Y_t$ adalah pengamatan pada waktu t
  • n adalah jumlah pengamatan yang dilakukan termasuk $EWMA_0$
  • $0≤\lambda≤1$ adalah konstanta yang menentukan memori EWMA

Roberts (1959).

Parameter λ menentukan kecepatan data yang lebih lama dihitung ke statistik EWMA. Nilai A value of $\lambda$ = 1 memberikan implikasi hanya data terbaru yang mempengaruhi EWMA. Jadi, semakin besar nilai λ (nilainya mendekati 1) akan membuat data terbaru lebih berpengaruh. Nilai λ yang kecil, mendekati 0, akan menyebabkan data yang lama lebih berpengaruh. Pada aplikasinya, biasanya nilai λ diatur antara 0.2 - 0.3. Lucas and Saccucci (1990) membuat tabel untuk memilih λ.

Diagram kendali EWMA untuk kadar air dalam biodiesel adalah sebagai berikut:

<pyspc: (8791187329677)>

CUSUM Control Chart

CUSUM (or cumulative sum control chart) adalah teknik analisis sekuensial yang dikembangkan oleh E. S. Page dari University of Cambridge. CUSUM biasanya digunakan untuk mendeteksi perubahan. Parameter $\theta$ disebut sebagai quality number yang mewakili distribusi probabilitas. Misalnya, nilai rata-rata digunakan sebagai $\theta$ maka CUSUM bisa digunakan untuk mengamati perubahan mendadak pada data berbasis waktu.
George Alfred Barnard metode visualisasi CUSUM yang disebut V-mask chart untuk mendeteksi perubahan $\theta$

rumus yang digunakan pada CUSUM adalah

$\S_{0} = 0$

$S_{n+1} = \max(0,S_{n}+x_n-\omega _n)S_{n+1}=\max(0, S_n+x_n-\omega_n)$

Ketika S melebihi nilai batas yang ditentukan, perubahan nilai dideteksi. Untuk perubahan ke arah negatif fungsi min digunakan pada persamaan di atas.

Untuk mengases kinerja CUSUM digunakan average run length (A.R.L.) metric, yang didefinisikan: "the expected number of articles sampled before action is taken.

Diagram kendali CUSUM untuk kadar air dalam biodiesel adalah sebagai berikut

<pyspc: (8791178873701)>

Shewhart X-bar dan S Control Chart

Kita harus menggunakan s-chart terlebih dahulu untuk menentukan apakah karakteristik distribusi proses stabil. Misalnya kita harus memperkirakan $σ$ dengan menganalisis data yang sudah diperoleh sebelumnya. Misalkan kita memiliki sampel awal sebanyak $m$, masing-masing tersusun dari $n$ data, dan $s_i$ adalah standar deviasi sampel ke-i. Maka rata-rata dari standar deviasi adalah

$$\bar{s} = \frac{1}{m} \sum_{i=1}^m s_i \, .$$

Kita akan menggunakan tabel c4 untuk perhitungan. Dengan $s/c_4$ sebagai unbiased estimator untuk σ maka diagram kontrol dapat dibuat dengan persamaan berikut:

$$\begin{eqnarray} UCL & = & \bar{s} + 3\frac{\bar{s}} {c_4} \sqrt{1 - c_4^2} \\ \mbox{Center Line} & = & \bar{s} \\ LCL & = & \bar{s} - 3\frac{\bar{s}} {c_4} \sqrt{1 - c_4^2} \, . \end{eqnarray}$$

Dengan langkah yang sama kita bisa membuat diagram kontrol untuk ${\bar{X}}$ sebagai berikut:

$$\begin{eqnarray} UCL & = & \bar{\bar{x}} + 3\frac{\bar{s}}{c_4\sqrt{n}} \\ \mbox{Center Line} & = & \bar{\bar{x}} \\ LCL & = & \bar{\bar{x}} - 3\frac{\bar{s}}{c_4\sqrt{n}} \, . \end{eqnarray}$$

Tabel untuk Control Chart

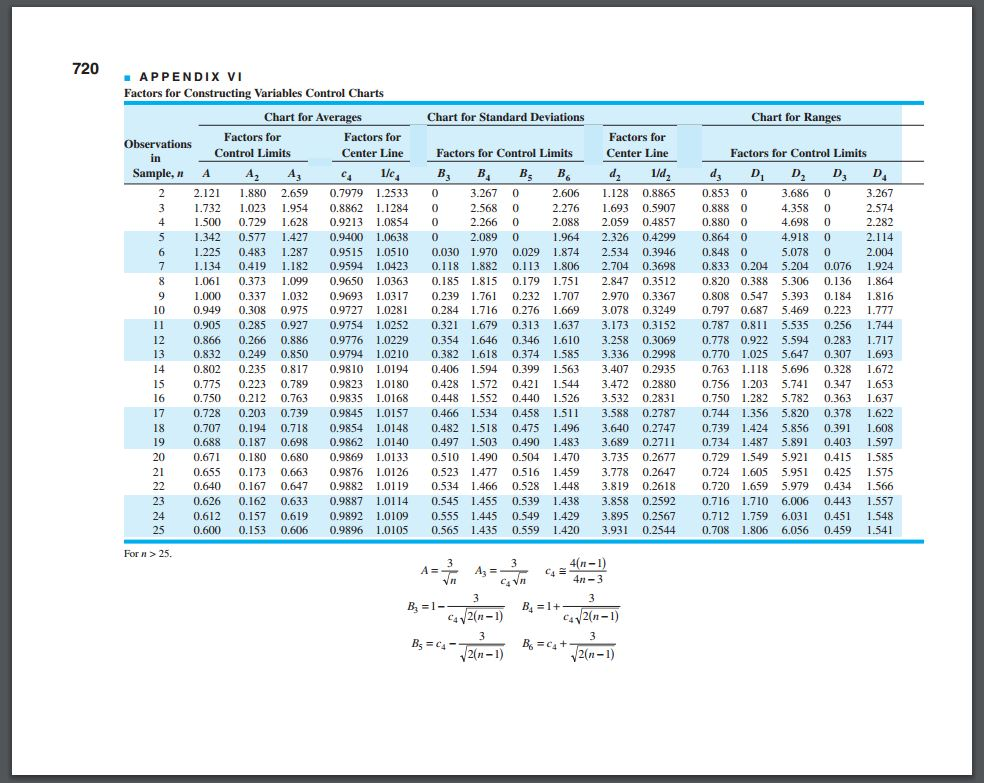
Diagram kendali ${\bar{X}}$ dan $S$ untuk pengukuran paracetamol adalah sebagai berikut

<pyspc: (8791187282305)>


<pyspc: (8791187390609)>

X dan R Control Charts

¯ Bila sampel relatif sedikit, misalnya kurang dari 10, kita bisa membuat rentang sampel untuk membuat diagram kontrol, bukan menggunakan simpangan baku.

Rentang sampel adalah perbedaan antara nilai pengamatan terbesar dan terkecil. Menurut Patnaik, 1946, ada hubungan statistik antara rata-rata rentang sampel untuk data yang terdistribusi normal dengan nilai $\sigma$, simpangan baku dari distribusi data. Hubungan ini hanya bergantung pada ukuran sampel, Rata-rata rentang, $R$, adalah $d_2 \sigma$ dimana nilai $d_2$ merupakan fungsi n, sehingga estimator untuk $\sigma$ adalah $R /d_2$.

Misalnya $R_1, R_2, R_3,...., R_k$ adalah rentang sampel k, rata-ratanya adalah

$$\bar{R} = \frac{R_1 + R_2 + ... + R_k} {k} \, .$$

Jadi, jika kita menggunakan ${\bar{X}}$ sebagai estimator $\mu$ dan ${bar{R}}/d_2$ sebagai estimator $\sigma$, maka parameter untuk ${\bar{X}}$ adalah

$$\begin{eqnarray} UCL & = & \bar{\bar{x}} + \frac{3}{d_2\sqrt{n}} \bar{R} \\ \mbox{Center Line} & = & \bar{\bar{x}} \\ LCL & = & \bar{\bar{x}} - \frac{3}{d_2\sqrt{n}} \bar{R} \, . \end{eqnarray}$$

dengan persamaan $A_2 = {3\over(d_2√n)}$ maka ${\bar{X}}$ menjadi

$$\begin{eqnarray} UCL & = & \bar{\bar{x}} + A_2 \bar{R} \\ \mbox{Center Line} & = & \bar{\bar{x}} \\ LCL & = & \bar{\bar{x}} - A_2 \bar{R} \, . \\ \end{eqnarray}$$

R Chart

Untuk menghitung batas kendali/kontrol kita perlu mengestimasi simpangan baku $w = R/\sigma$
Simpangan baku W adalah $d_3$ yang merupakan fungsi sampel n. Karena $R = W \sigma$ maka simpangan baku R adalah $\sigma_R = d_3 \sigma$ karena $\sigma$ tidak diketahui kita bisa mengestimasi menggunakan persamaan:

$$\begin{eqnarray} UCL & = & \bar{\bar{x}} + A_2 \bar{R} \\ \mbox{Center Line} & = & \bar{\bar{x}} \\ LCL & = & \bar{\bar{x}} - A_2 \bar{R} \, . \\ \end{eqnarray}$$

Sehingga R chart dengan metode 3 sigma adalah

$$\begin{eqnarray} UCL & = & \bar{R} + 3\hat{\sigma_R} = \bar{R} + 3d_3\frac{\bar{R}}{d_2} \\ \mbox{Center Line} & = & \bar{R} \\ LCL & = & \bar{R} - 3\hat{\sigma_R} = \bar{R} - 3d_3\frac{\bar{R}}{d_2} \, . \end{eqnarray}$$

Dengan $D_3 = 1 - 3 d_3/d_2$ dan $D_4 = 1 + 3 d_3/d_2$

$$\begin{eqnarray} UCL & = & \bar{R} D_4 \\ \mbox{Center Line} & = & \bar{R} \\ LCL & = & \bar{R} D_3 \, . \end{eqnarray}$$
n A2 D3 D4
0 2 1.880 0.000 3.267
1 3 1.023 0.000 2.575
2 4 0.729 0.000 2.282
3 5 0.577 0.000 2.115
4 6 0.483 0.000 2.004
5 7 0.419 0.076 1.924
6 8 0.373 0.136 1.864
7 9 0.337 0.184 1.816
8 10 0.308 0.223 1.777

Hubungan efisiensi penggantian R dengan s/c4 dipengaruhi oleh jumlah n

n Efisiensi Relatif
0 2 1.000
1 3 0.992
2 4 0.975
3 5 0.955
4 6 0.930
5 10 0.850

Dengan demikian, sampel dengan ukuran di bawah 5 tidak akan memberikan perbedaan yang relatif besar.

Diagram kendali ${\bar{X}}$ dan $R$ untuk pengukuran paracetamol adalah sebagai berikut

<pyspc: (8791178709017)>


<pyspc: (8791178644561)>